Conical and pyramidal shapes are often used, generally in a truncated form, to store grain and other commodities. Similarly a silo in the form of a cylinder, sometimes with a cone on the bottom, is often used as a place of storage. It is important to be able to calculate the volume and surface area of these solids. These solids differ from prisms in that they do not have uniform cross sections. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cn and its height is 180 cm.
Using the volume formulas for these shapes allows us to compare the volume of different types of objects, sometimes with surprising results. Now the question becomes calculating the volume of the bicylinder . It is also very difficult, so add a cube packing the bicylinder . Now when the plane intersects the cube, it forms another larger square. The extra area in the large square , is the same as 4 small squares . Moving through the whole bicylinder generates a total of 8 pyramids.
A glass dome for a lighting fixture is in the shape of a hemisphere. The circumference of the great circle of the hemisphere is 12π inches. Which statements about the hemisphere are true? The total surface area is 108π square inches. The total surface area is 144π square inches. The total surface area is 432π square inches.
The total surface area is 36π square inches. A sphere is the shape of a basketball, like a three-dimensional circle. Just like a circle, the size of a sphere is determined by its radius, which is the distance from the center of the sphere to any point on its surface. The formulas for the volume and surface area of a sphere are given below. Calculating volume and surface area of sphere play an important role in mathematics and real life as well.
Formulas for volume & surface area of sphere can be used to explore many other formulas and mathematical equations. The baseball is not regulation size. If the baseball has a surface area of 9π, then I can set that equal to the formula 4πr2 and solve for r.
The radius is 3/2 inches, so I double that to find the diameter. The diameter of the ball is 3 inches, which is greater than the allowed range of diameters. This statement is not at all obvious or elementary. "A sphere's volume is two cones of equal height and radius to that of the sphere's". The assertion about the cone and the cylinder is a little easier to prove, but it too is not obvious.
So you have not really provided an answer to this to year old question. I think the accepted answer is closest to what you have in mind. If you want to help here I think you should pay attention to new questions that don't yet have answers.
The following video shows how to solve problems involving the formulas for the surface area and volume of spheres. Q.9.A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as show in Fig. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article. Q.5.A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube.
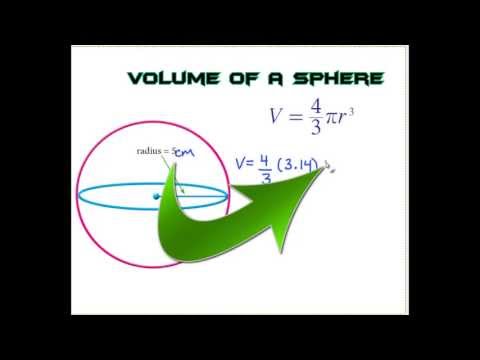
Determine the surface area of the remaining solid. A sphere is a three-dimensional, round object, such as a marble or soccer ball. The volume represents the space enclosed by the object. The formula for the volume of a sphere is 4/3 times pi times the radius cubed. Cubing a number means multiplying it by itself three times, in this case, the radius times the radius times the radius. To find the volume in terms of pi, leave pi in the formula rather than converting it to 3.14.
For any other value for the length of the radius of a sphere, just supply a positive real number and click on the GENERATE WORK button. They can use these methods in order to determine the surface area and volume of parts of a sphere. If you ever wondered what's the volume of the Earth, soccer ball or a helium balloon, our sphere volume calculator is here for you. It can help to calculate the volume of the sphere, given the radius or the circumference.
Also, thanks to this calculator you can determine the spherical cap volume or hemisphere volume. It will also give the answers for volume, surface area and circumference in terms of PI π. A sphere is a set of points in three dimensional space that are located at an equal distance r from a given point . Suppose you have two solid figures lined up next to each other, each fitting between the same two parallel planes.
(E.g., two stacks of pennies lying on the table, of the same height). Then, consider cutting the two solids by a plane parallel to the given two and in between them. If the cross-sectional area thus formed is the same for each of the solids for any such plane, the volumes of the solids are the same.
There is another special formula for finding the volume of a sphere. The volume is how much space takes up the inside of a sphere. The answer to a volume question is always in cubic units. Take a hemisphere of radius and look at the area of a typical cross-section at height above the base. Q.1.A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius.
Find the volume of the solid in terms of π. A sphere is a three-dimensional solid with no base, no edge, no face and no vertex. Sphere is a round body with all points on its surface equidistant from the center. The volume of a sphere is measured in cubic units. The volume of a sphere is the three-dimensional space occupied by a sphere. This volume depends on the radius of the sphere (i.e, the distance of any point on the surface of the sphere from its centre).
If we take the cross-section of the sphere then the radius can be calculated by reducing the length of the diameter to its half. Or we can also say that the radius is half of the diameter. A circle can be drawn on a paper but a sphere can't be drawn on a piece of paper. This is because Circle is a two-dimensional figure whereas a sphere is a three-dimensional object, example- Ball, Earth, etc. A Sphere is a 3D figure whose all the points lie in the space.
All the points on the surface of a sphere are equidistant from its centre. This distance from the surface to the centre is called the radius of the sphere. I can solve mathematical and real-world problems about the volume of cylinders, cones, and spheres. A regulation baseball must have a diameter between 2.87 and 2.94 inches.
The surface area of a particular baseball is 9π square inches. Is the baseball within the range of regulation size? A globe of Earth is in the shape of a sphere with radius 14[/latex] centimeters.
Round the answer to the nearest hundredth. In this lesson, you'll learn how to find the volume of a sphere with a radius of 4 inches. A sphere is a 3-dimensional round object. The volume is how space is inside the sphere. When you want to find out how much space is inside such a sphere, you'll follow these steps to calculate the volume of the sphere. A sphere is a three-dimensional solid with no face, no edge, no base and no vertex.
It is a round body with all points on its surface equidistant from the center. Browse other questions tagged geometry volume solid-geometry spheres or ask your own question. The following figure gives the formula for the volume of sphere.
Scroll down the page for examples and solutions. Calculus is needed to derive the formula for the surface area of a sphere rigorously. Here is a interesting formula that uses the idea of approximating the sphere by pyramids with a common vertex at the centre of the sphere.
Q.2.Metallic spheres of radii 6 cm, 8 cm and 10 cm, respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere. Q.6.A solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm3 of iron has approximately 8 g mass.
Q.3.A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy. Q.2.A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder.
The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel. A spherical solid metal of a radius of $16$ inches is melted down into a cube. What will be the dimensions of the cube?
Use $\pi \approx 3.14$ and estimate your answer to the nearest whole number. Half of the Sphere is called Hemisphere. A sphere is defined as a set of three-dimensional points and the centre is equidistant with all the points on the surface. Just for say, when an aircraft takes a round of the earth from earth's midpoint, it covers two hemispheres of the earth. It can be said that the globe is made of two hemispheres. A globe generally produces two hemispheres exactly.
Our earth is composed of two hemispheres, the southern and the northern hemispheres. If a solid sphere is cut and taken out of a big solid sphere, leaving behind a thin surface in the form of a spherical shell is called Hollow sphere. It is more like a balloon or ball filled with air. A sphere is a perfectly round solid figure. All points on the surface of the shape are the same distance away from the centre – we call this distance the radius.
Volume of the basic solids like cuboids, cubes, cylinders, cones and sphere... The surface area of the zone or frustum is equal to the circumference of the great circle of the sphere times the altitude of the same. 7Given a solid sphere of radius R, remove a cylinder whose central axis goes through the center of the sphere. Well I wasn't really going for elementary, just a dumbed down version that worked for me that might help others starting at University Math. The other answers were great with backgrounds of why a sphere fits into a cylinder, etc, so I left that part out of mine. I personally wasn't able to figure out where 4/3 came from using any of their answers, so I contributed mine to help those that may see things my way.
I agree it is an old question, but I had this question in 2019 that I couldn't find the answer to with those answers. A sphere can be formed by revolving a semicircle about is diameter edge. Since it is already known that the volume of a sphere is 4/3 Pi radius cubed, all that is left is to replace all the variables in the formula. Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.
The volume of a hemisphere is equal to two-thirds of the product of pi and the cube of the radius. Use Cavalieri's principle to deduce that these solids have the same volume and hence find derive the formula for the volume of the sphere. We can then integrate this to obtain the total volume. This method can be used very effectively to find the volume of solids which do not have uniform cross-section, and may have curved boundaries. Q.6.Derive the formula for the curved surface area and total surface area of the frustum of a cone, given to you in Section 13.5, using the symbols as explained. Q.1.A drinking glass is in the shape of a frustum of a cone of height 14 cm.
The diameters of its two circular ends are 4 cm and 2 cm. Q.5.A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm.
It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-forth of the water flows out. Find the number of lead shots dropped in the vessel.